Risk: Crooked Values

Part 2 of an intermittent series babbling on about Mark Spitznagel's Safe Haven.

"Improvement makes strait roads, but the crooked roads are works of genius." — William Blake

One thing I love about reading this sort of book from this type of widely-read—erudite, even—author is that they align insights which can be mathematically derived from one niche field (finance, in this case) with principles that can be signposts for other aspects of life as well. This is easy to see here, as Spitznagel draws illustrative points from philosophy of science (Aristotle, Karl Popper) as well as mathematicians (the many Bernoulli's) and even more of what we might call “pure” philosophers (Nietzsche).

The key insight I am taking from these early sections of the book is that investing—like life itself—is a process, which unfolds sequentially through time. It’s a multi-period, iterative, multiplicative experience. One’s experiences compound—meaning that the end state of the previous day is the starting point for the current day. While the explicit goal of investing is to maximize wealth over time, it’s not hard to translate a “growth mentality” (are we still using that phrase, or have tiktok influencers poisoned the well?) into other domains. Eudaimonia, in one’s own life, for instance—humane flourishing. Server uptime and responsiveness, in the software-as-a-service world. Whatever your metric is. Think geometrically about that metric.

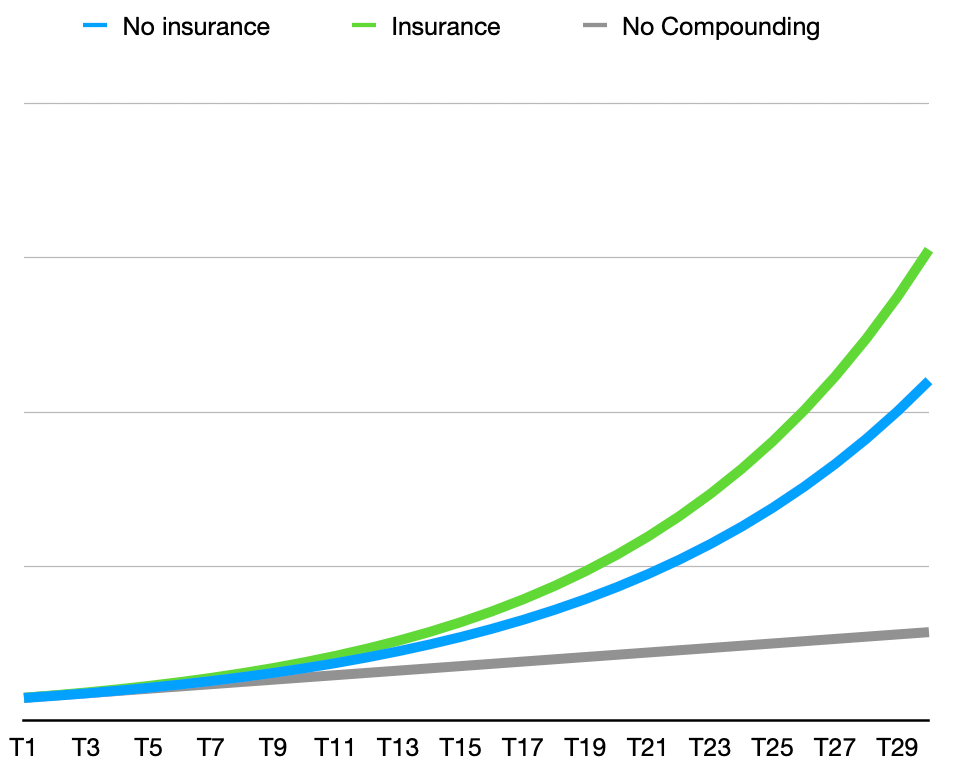
Additive risk-mitigation increases the value obtained over time, even as it might cost money in each period. This is the cost-effectiveness that Spitznagel is looking for: sort of a “first derivative” view—the whole point here isn’t just to spend resources lowering risk in an absolute sense; it’s to do so in such a way that the systemic returns are greater than they would be otherwise. The objective here is pragmatic, not academic—risk managers should be able to point at a scoreboard rather than an abstract or model.

Values, expected and otherwise

The value of any given thing is relative to how much of it we already have.

The trick with risk is to move our traditional mode of thinking from the linear to the geometric or non-linear when assessing risk in complex systems. Most of us, as individuals or even organizations, are exposed to such a small real-world sample size that we aren’t covered by the “mediocristan” law of large numbers. We get to walk one path—we’re the gambler who must “go to war with luck”, rather than the casino who can ride more or less comfortably with a vast set of trials where the arithmetic average gradually wins out.

A Swiss mathematician (one of many, apparently) named Bernoulli made perhaps the first such change-up when he used a geometric average to calculate EV instead of the arithmetic average. This is significant, because many more real-world risk scenarios are geometric rather than linear, especially in an increasingly complex world. To oversimplify this point—and I think this is starting to get across—one has to check the median as well as the average. On average, U.S. Presidents have now been charged with slightly over 2 felonies each. But the median President has been charged with 0.

Or, to consider a hard-headed case of insurance underwriting in the Baltic Sea mercantile trade, I can’t do better than this animated explainer from Universa, Spitznagel’s own company. It’s pretty eye opening—this sort of risk management is not only arithmetically a pure cost while being a geometric (i.e. time-series) value-add, but it is also not zero-sum. The insurer makes money and the merchant makes more money than they would without.

An inconvenient, uncomfortable but crucial truth: your raw, linear returns are a lie; your true returns are crooked.

We’re so used to thinking in linear terms that it is hard to intuitively grasp geometric, non-linear risk. This error usually ends up exposing more of our principal to loss. In investing, as in life, the more of your principal—whatever that happens to be—you lose, the harder and less likely you will be to recover fully. The consequences of going to zero might be your life; of infinite value. So the corollary to all of these points is “Profit is finite. (Downside) Risk is infinite." Look out for waterfalls on the river of life.

Unless you’re a “law of large numbers” institution, you get what you get, not what you expect. Your N is 1—there’s a single life path out of all the many options. Ergo the your internal value proposition should shift towards an understanding "that getting the value of this path right eclipses the value of getting the expected value right.”

I feel like I’m just plundering sections of the book at this point, so I’ll leave you with one last quote that sums so very, very much up:

“The task is to live in such a way that you must wish to live it again.” — Nietzsche